How do different aspects of the input metocean data affect Mermaid results?
There are a range of sources of variability when it comes to putting together a Mermaid analysis, and they can all affect the output statistics to various degrees. It could be subtle changes such as weather thresholds, task durations or the level of suspendability; or more strategic changes such as vessel and port choice. But that’s what Mermaid is designed for, for you to be able to tweak and optimise your operation to minimise the weather risk.
However, there are other aspects that may affect the results which are not operation related and that users may not have considered. These are the duration of metocean data, the frequency of start date repeats and the time step of the metocean data. The first two will directly influence the number of operation simulations and hence the amount of data that make up the output statistics and the third one will influence how well high frequency variability in the weather conditions is accounted for.
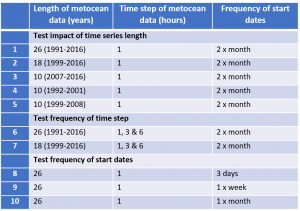
To consider the effect of these factors we have carried out a few tests. We have taken a single time series of high quality metocean data (hourly, 26-years) and run the same Mermaid analysis multiple times but with different time-step and start date specifications. The different tests are summarised in the table below:
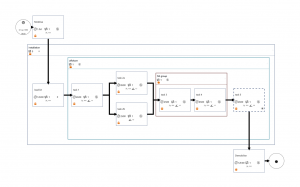
The operation modelled is a relatively straight forward one with nine tasks of varying thresholds, durations and suspendability, and all repeated at five sites of close proximity. The total unweathered duration is just short of 11 days. The task flow diagram is shown below:
Test 1: Impact of time series duration
The first test has consisted of running the above operation with 26, 18 and 10 years of data. The time series data is hourly, and there have been two start dates per month. We have used three different 10-year periods (1992-2001, 1999-2008 and 2007-2016) to see what impact this makes.
The figure below shows the duration Box and Whisker plot for the five different analyses, with the P50’s focused on in the embedded plot.
If we look at just the P50 durations there is actually little variation between the results, the main feature being the slightly higher values from the 10-year (1992-2001) data. Across all P50 analyses, the biggest difference in a month is 2.5 days, however, between the 26-year and 18-year datasets the biggest difference is only 0.9 days.
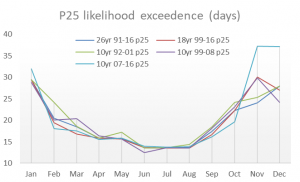
There is more variability when looking at the longer durations that have the lower likelihoods of occurrence (top of the box (25th %ile) and the whisker (max)). This variability occurs mostly in the autumn and winter months. For example, in November the P25 when using 26-years of data is 24 days. However, if we had used data from 2007-2016 only, then the P25 is 37 days. For an 11-day operation, this is a difference of between 13 and 26 days’ downtime.
However, the key characteristic that stands out is the variability between the results that come from the different 10-year datasets. The results from 2007-2016 show a much bigger risk of longer operation lengths in November and December than any of the other simulations. For example, the December P25 is 37 days compared to 24 and 28 days if using the 1999-2008 or 1992-2001 data respectively. Paradoxically, the reverse trend occurs in October, where the P25 based on 2007-2016 data is 19.5 days compared to 23 and 24 days from the other 10-year periods.
What these results highlight is the variability present in the annual and decadal cycles of the weather that impacts northwest Europe. The different 10-year periods clearly have different features with some having stormier seasons than others and so produce noticeably differing statistics. With only 10-years to sample from, it only takes one or two unusual years to skew the results.
Whilst the P50 statistics are relatively consistent, this all adds to the evidence that you want to be using as long a dataset as possible when running Mermaid simulations.
Test 2: The impact of the time series time step
The second aspect of a time series that we have looked at is the time-step of the data. The concern with using data with large time-steps is that you will have a much smoother profile of wind and wave data, and may not be capturing the higher frequency events that could be breaching your operational thresholds. If you have tasks that are only 15-30 minutes long, and you are interpolating a 6-hour dataset down to 15 minutes, you are introducing some significant assumptions about the data and will possibly not be simulating your operation against realistic conditions.
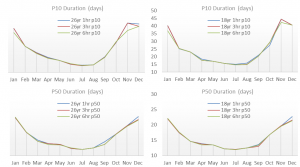
To investigate this further we have run the same operation as before against the 18-year and 26-year datasets but with time-steps of 1, 3 and 6 hours. We have not used the 10-year datasets as the variability introduced by having a short time series will likely mask any differences introduced by the time-step changes.
The line graphs above show the P10 and P50 duration statistics for all 6 analyses. The results in this case are a little surprising as they show there is little difference in durations when using time series of different time-steps. The only noticeable difference occurs in November, where the results based on 26 years, 6-hourly data produces a P10 value that is 5 days shorter than the 3-hourly and hourly datasets. Looking further at the raw outputs shows that, in fact, 10% of the simulations had a difference in operation duration of more than two days, and 4% greater than 5 days. There are a number individual occasions where the difference in time series affects the Mermaid analysis, but for most of cases it appears negligible.
Whether this is the case for different time series data at different locations or for different analyses remains to be seen.
Test 3: Impact of the frequency of analysis start date
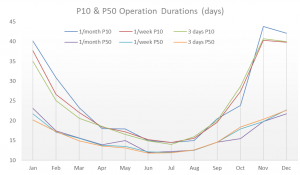
The final comparison made is between the results of Mermaid analyses that have different frequencies of start dates, either sampling once a month, once a week or every three days. For an eleven day operation, it is anticipated that the number of times per month the operation is tested should have an impact on the duration statistics. For example, an operation started on the 1st of the month will run into a different population of weather data to one started on the 15th. As the number of start dates is increased, it is likely that the same weather data is sampled more than once and so operation length statistics will start to converge and vary less.
The figure here shows the monthly P10 and P50 operation durations for the three different start date settings. There is certainly more variability here than the results from the time step comparison, but the differences are not striking. The analysis that repeats the start date every three days produces 3151 simulations, compared to only 311 when started once a month. This higher number of samples produces a smoother profile and lower P10 values, but not dissimilar P50’s. There is less of a difference between the 3-day start date repeat and the once a week start date, suggesting the later samples enough of the weather data to provide similar statistics.
Conclusions
It must be noted that this has not been a full in-depth study. To satisfy our own curiosity we have run a range of different scenarios through Mermaid to see what differences occur when the input time series is varied. To have further confidence in the results it would be sensible to repeat the analyses at different locations and vary the makeup of the operation tasks.
The most useful output from this small experiment has been the confirmation that it is the overall length of input time series that can have the biggest impact, especially when looking at the tail of the distribution of operation lengths. What has been particularly interesting is the variability in the results when using different 10-year periods. This highlights the inter-annual and decadal variability that exists in the weather patterns that impact the north west European waters – one ten-year period can be quite different to another. For this reason, if you are planning an operation that is particularly sensitive and need to get a good grasp of the potential extreme downtime then be prudent with the amount of metocean data that you use.
What has also been particularly interesting is the lack of sensitivity to the time step frequency of the data. Operation length statistics based on six-hourly data has compared very closely to one-hourly data. In this case, the weather data does not seemingly vary quickly enough that using a smoother profile data set reduces the accuracy of the downtime predictions.
Finally, in this example, there is only a moderate impact when varying the start date frequency. Clearly with a higher number of samples the output statistics are of a higher confidence, but still show a similar trend to when less data is used. The importance of the start date frequency will vary depending on the overall operation length; if you’re modelling a 20-day operation, you won’t need to test a start date every 2 or 3 days. Conversely, if you’re modelling a short operation then you will not be making the most of your metocean data if you have only one start date a month.
If you want to discuss data options for your own Mermaid analyses then please do get in touch and we can advise.